Quantum computing is an advanced paradigm of computation

 Quantum computing is an advanced paradigm of computation that utilizes the principles of quantum mechanics to perform computations beyond the capabilities of classical computers. While classical computers represent data using bits (either 0 or 1), quantum computers use quantum bits or qubits that can exist in a superposition of both 0 and 1 states. This unique property of superposition allows quantum computers to solve certain problems exponentially faster than classical counterparts. In this comprehensive overview, we'll explore the fundamentals of quantum computing, its underlying principles, quantum algorithms, current technologies, challenges, and potential applications.

 Introduction to Quantum Computing

   - Brief history and key milestones in quantum computing development

   - Comparison of classical and quantum computers.

   - Explanation of qubits and their unique properties (superposition and entanglement).

   - Importance of quantum parallelism in speeding up computations.

Quantum computing is an area of computing that utilizes the principles of quantum mechanics to process information in a fundamentally different way than classical computers. Here's a brief history of quantum computing development and key milestones:

Origins of Quantum Mechanics 

   The foundation of quantum mechanics was laid by physicists such as Max Planck, Albert Einstein, Niels Bohr, and others in the early 20th century. Their work led to the understanding that particles at the quantum level can exist in multiple states simultaneously, known as superposition, and can be entangled with one another.

 Birth of Quantum Computing 

   In 1981, physicist Richard Feynman first suggested the concept of quantum computing as a way to simulate quantum systems efficiently, which would be intractable for classical computers. A few years later, in 1985, David Deutsch proposed the first quantum computing model known as the "universal quantum Turing machine."

 Quantum Algorithms

   In 1994, mathematician Peter Shor developed the famous Shor's algorithm, demonstrating that quantum computers could efficiently factor large numbers, posing a significant threat to widely-used classical cryptographic systems. Around the same time, Lov Grover devised Grover's algorithm, a quantum search algorithm providing a quadratic speedup compared to classical search algorithms.

First Quantum Algorithms Implementations

   In the early 2000s, experimentalists started to implement basic quantum algorithms on small-scale quantum computers. IBM, NIST, and other research institutions were among the pioneers in this field.

 Quantum Error Correction

   Quantum systems are sensitive to noise and decoherence, which can cause errors in computations. Quantum error correction theory emerged to address these issues. In 1996, Peter Shor and Andrew Steane independently proposed quantum error-correcting codes.

 D-Wave's Quantum Annealer

   D-Wave Systems introduced its first commercially available quantum annealer in 2007, aiming to solve optimization problems. However, the debate continues whether D-Wave's early devices provide a true quantum advantage compared to classical computers.

IBM's Quantum Experience

   In 2016, IBM launched the IBM Quantum Experience, an online platform allowing users to access and run experiments on a cloud-based quantum computer. This initiative provided widespread access to early-stage quantum computing.

Google's Quantum Supremacy

   In 2019, Google claimed to achieve "quantum supremacy" by demonstrating their 53-qubit quantum processor, Sycamore, performing a specific task significantly faster than the most advanced classical supercomputers.

 Quantum Hardware Advancements

   Since the late 2010s and early 2020s, various tech companies and research institutions have been continuously improving quantum hardware, increasing the qubit count, reducing errors, and improving coherence times.

 Quantum Algorithm Progress 

   Researchers have been working on developing and optimizing various quantum algorithms to showcase the advantage of quantum computing over classical counterparts. Notable advancements include better quantum error-correction techniques and applications in fields like cryptography, optimization, and machine learning.

Quantum Mechanics Essentials

   - Overview of quantum mechanics principles, including wave-particle duality, uncertainty principle, and quantum measurement.

   - Introduction to Dirac notation and quantum states.

   - Explanation of unitary operators and how they evolve quantum states.

   - Quantum gates and their role in quantum circuitry.

Quantum mechanics is a fundamental branch of physics that deals with the behavior of matter and energy at the smallest scales, such as atoms and subatomic particles. It provides a mathematical framework to describe the peculiar behavior of these particles, which often defies our classical intuitions.

Wave-Particle Duality

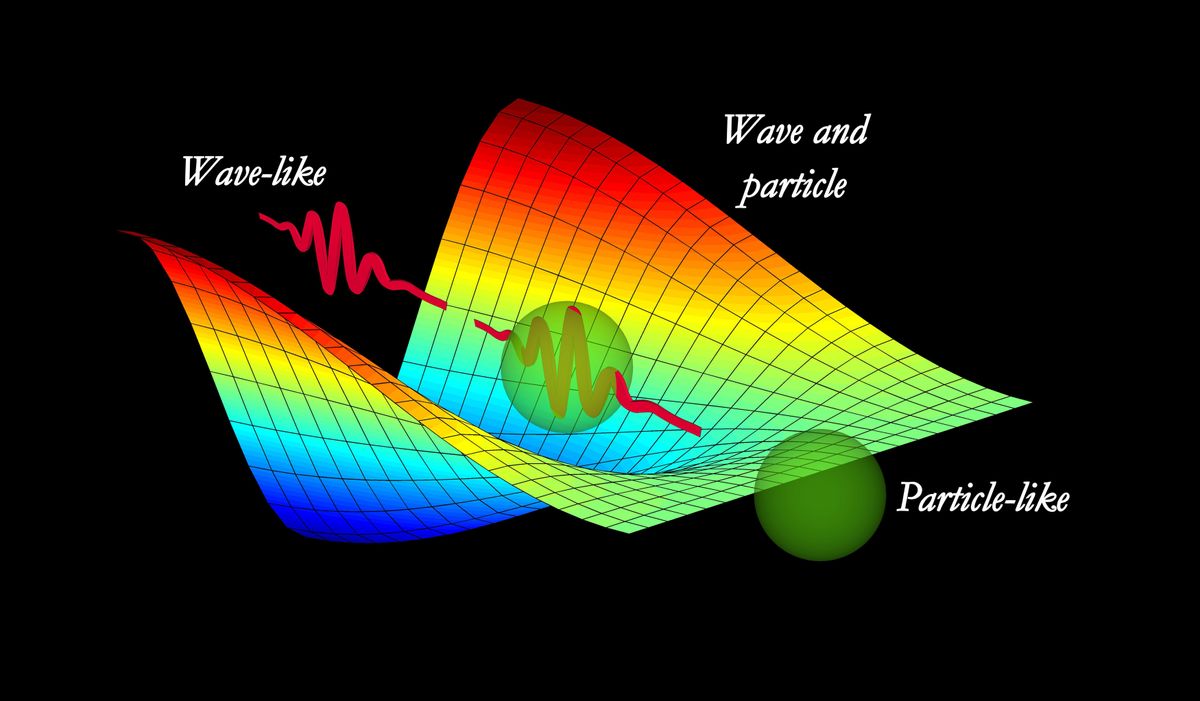
One of the most intriguing principles of quantum mechanics is the wave-particle duality. It states that particles, like electrons and photons, can exhibit both wave-like and particle-like properties depending on the experimental context. This means that particles can behave as discrete, localized entities (particles) and also as continuous, spread-out waves.

This duality was first proposed by Louis de Broglie in 1924 and was experimentally verified through the famous double-slit experiment. In this experiment, particles (e.g., electrons) are sent through a barrier with two slits. The resulting interference pattern on the screen behind the slits shows wave-like behavior, suggesting that particles can interfere with themselves like waves do. However, when the particles are observed, they behave as distinct particles and lose their wave-like characteristics.

Uncertainty Principle (Heisenberg Uncertainty Principle)

The uncertainty principle, formulated by Werner Heisenberg in 1927, states that there is a fundamental limit to the precision with which certain pairs of complementary properties of a quantum system can be simultaneously known. The complementary properties typically involve position and momentum or energy and time.

Mathematically, the uncertainty principle is expressed as Δx * Δp >= ħ/2, where Δx represents the uncertainty in position, Δp represents the uncertainty in momentum, and ħ is the reduced Planck constant (h-bar). This principle implies that the more precisely you measure one of these properties, the less precise your measurement of the other property will be. It highlights the inherent probabilistic nature of quantum mechanics and challenges our classical notions of definite states.

Quantum Measurement

Quantum measurement is a crucial concept in quantum mechanics and is intimately related to the wave function collapse. The wave function describes the probability distribution of a quantum system, and it evolves in time according to the Schrödinger equation, which is a fundamental equation in quantum mechanics.

When a quantum system is measured, it "collapses" into one of its possible states with definite properties. The outcome of the measurement is probabilistic, and the probability of finding the system in a particular state is given by the squared magnitude of the wave function (Born rule). This process is often non-deterministic and random, leading to different outcomes for identical measurements.

The measurement process is a subject of debate and interpretation in quantum mechanics, giving rise to various interpretations, such as the Copenhagen interpretation, many-worlds interpretation, and more.

These principles of quantum mechanics have revolutionized our understanding of the microscopic world and have led to numerous technological advancements, such as quantum computing, quantum cryptography, and precision measurement devices. Despite their abstract nature, these principles form the foundation of modern physics and play a crucial role in shaping our understanding of the universe.

. Quantum Algorithms

   - Quantum superposition and its importance in algorithm design.

   - Overview of quantum algorithms: Deutsch-Jozsa, Grover's, Shor's, and quantum simulation algorithms.

   - Quantum Fourier Transform and its significance in many quantum algorithms.

   - Explanation of how quantum algorithms achieve speedup compared to classical counterparts.

Quantum mechanics is a fundamental branch of physics that deals with the behavior of matter and energy at the smallest scales, such as atoms and subatomic particles. It provides a mathematical framework to describe the peculiar behavior of these particles, which often defies our classical intuitions.

Quantum Hardware Technologies

   - Different types of qubits: superconducting circuits, trapped ions, topological qubits, and others.

   - Quantum error correction and the challenge of qubit decoherence.

   - Quantum gates and quantum circuit implementations.

   - Quantum computing architectures and quantum processors.

 Different Types of Qubits

Qubits are the fundamental building blocks of quantum computers, and they can be realized using various physical systems. Some of the most promising types of qubits include:

Superconducting Qubits: These are circuits made of superconducting materials, such as Josephson junctions. Superconducting qubits are currently among the leading candidates for building quantum processors due to their relative ease of fabrication and scalability.

Trapped Ion Qubits: In this approach, qubits are encoded in the internal energy levels of trapped ions, typically using laser manipulation for quantum operations. Trapped ions have shown high fidelity and long coherence times, making them another promising candidate for quantum computing.

 Topological Qubits: Topological qubits are theoretical qubits that rely on certain exotic properties of topological states of matter to achieve fault-tolerant quantum computation. Examples include Majorana qubits, which are anyons with non-Abelian statistics.

Photonic Qubits: Photons can be used as qubits by encoding quantum information in their polarization, path, or other degrees of freedom. Photonic qubits have the advantage of low interaction with the environment, making them relatively robust against decoherence.

 Quantum Dot Qubits: Quantum dots are semiconductor nanostructures that can trap single electrons, and their spin states can serve as qubits. Quantum dots offer potential for integration with existing semiconductor technology.

 NV Center Qubits: NV (Nitrogen-Vacancy) centers in diamonds can be used as qubits by exploiting the spin states of nitrogen atoms associated with a vacancy in the diamond lattice.

Quantum Error Correction and Qubit Decoherence

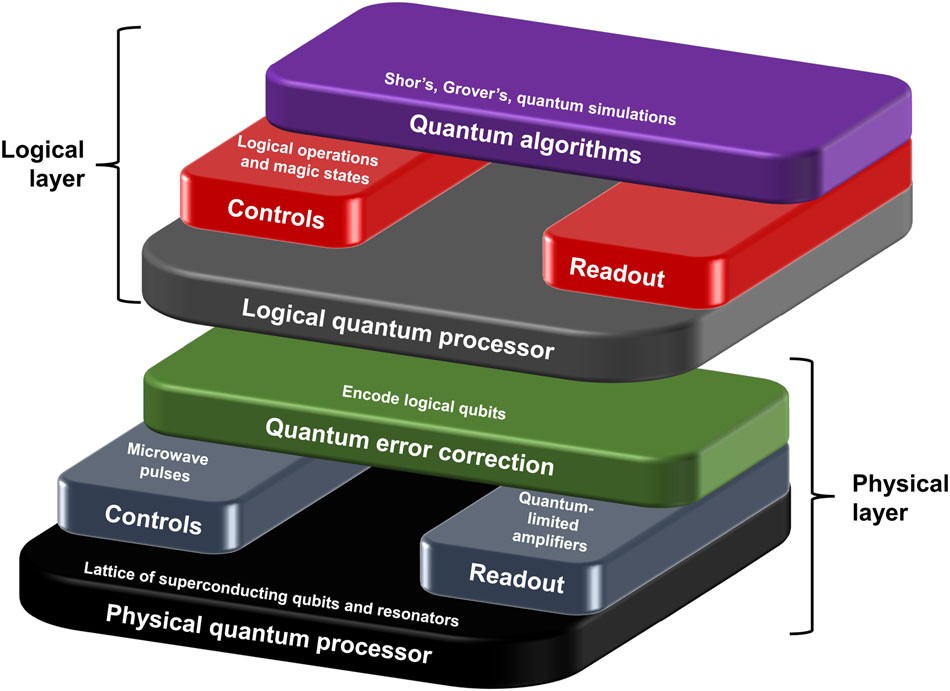
Quantum error correction is a set of techniques used to protect quantum information from errors and decoherence that inevitably affect qubits due to their interaction with the environment. Decoherence is a major challenge in quantum computing, as quantum systems are extremely sensitive to their surroundings, leading to the loss of quantum coherence and information.

Quantum error correction employs quantum codes that encode quantum information redundantly in a way that allows the detection and correction of errors. These codes introduce additional qubits (ancillary qubits) that store information about the errors, allowing for error detection and correction. Quantum error correction is vital for scaling quantum computers and building fault-tolerant systems, where errors can be significantly reduced or even corrected.

 Quantum Gates and Quantum Circuit Implementations

Quantum gates are the basic operations that manipulate qubits in quantum circuits to perform quantum computations. These gates are analogous to classical logic gates but work on quantum states.

Some common quantum gates include:

   - Hadamard gate (H): Creates superposition.

   - Pauli gates (X, Y, Z): Rotations around the x, y, and z axes on the Bloch sphere.

   - CNOT (Controlled-NOT) gate: A two-qubit gate that performs a NOT operation on the target qubit if the control qubit is in the |1⟩ state.

Quantum circuits are sequences of quantum gates that represent quantum algorithms. These circuits take input qubits and apply a series of gates to manipulate and transform the quantum state, eventually leading to the desired output.

Quantum Computing Architectures and Quantum Processors

Quantum computing architectures refer to the physical layouts and connections of qubits within a quantum processor. Different quantum computing technologies adopt various architectures to implement quantum gates and enable qubit interactions. Some common architectures include:

   a. Linear Nearest-Neighbor Architectures: Qubits are arranged in a linear chain, and quantum gates can interact only between adjacent qubits. This architecture is commonly used in trapped ion and superconducting qubit systems.

   b. Grid Architectures: Qubits are organized in a two-dimensional grid, enabling more flexible qubit interactions. This architecture is common in some superconducting and trapped ion systems.

   c. Surface Code Architectures: These architectures are specifically designed for implementing quantum error correction codes, like the surface code, which is a two-dimensional grid of physical qubits with error correction features.

   d. Topological Quantum Computing Architectures: These architectures are designed to exploit topological properties of qubits to achieve fault-tolerant quantum computation.

5. Quantum Software and Programming

   - Introduction to quantum programming languages, such as Qiskit and Cirq.

   - Quantum algorithms expressed through quantum circuits.

   - Hybrid quantum-classical algorithms and their practicality.

   - Quantum compilation and optimization techniques.

Qiskit

Qiskit is an open-source quantum computing framework developed by IBM. It provides tools for working with quantum circuits, quantum algorithms, and quantum systems. Qiskit is written primarily in Python and offers a user-friendly interface for quantum programming. It consists of several components:

   - Terra: The foundation of Qiskit that provides a collection of tools for working with quantum circuits and gates.

   - Aer: A high-performance simulator backend that allows simulation of quantum circuits on classical computers.

   - Aqua: A library for quantum algorithm research and development, especially for quantum machine learning applications.

   - Ignis: A module for studying and mitigating noise on real quantum hardware.

   - IBM Quantum Experience (IQX): An online platform that allows users to run their Qiskit programs on actual IBM Quantum hardware.

Cirq

Cirq is another open-source quantum programming framework developed by Google. It is written in Python and is designed to provide a more low-level, circuit-centric approach to quantum programming. Cirq allows developers to define quantum circuits using native gates and operations supported by quantum processors. It aims to be more explicit and gives users fine-grained control over quantum circuits, which can be beneficial for certain types of quantum algorithms and research.

6. Quantum Communication and Cryptography

   - Quantum key distribution and secure communication using quantum entanglement.

   - Quantum-safe cryptographic algorithms and their importance in a post-quantum computing era.

   - Quantum teleportation and its implications for communication.

7. Quantum Simulation and Optimization

   - Quantum simulation for studying quantum systems and materials.

   - Variational quantum algorithms for optimization problems.

   - Quantum annealing and its role in solving combinatorial optimization problems.

8. Quantum Supremacy and Beyond 

   - Overview of Google's quantum supremacy demonstration.

   - The debate over the significance of quantum supremacy and its implications.

   - Quantum computing's potential impact on various industries, such as finance, healthcare, and logistics.

9. Challenges and Limitations

   - Quantum error correction and fault tolerance challenges.

   - The challenge of scaling quantum computers to larger systems.

   - Physical and engineering barriers to building practical quantum computers.

10. Future Outlook

    - Current state of quantum computing research and development.

    - The potential for quantum computing to revolutionize various fields.

    - Speculations about the future direction of quantum computing.

 the field of quantum computing was rapidly advancing, but it's important to note that there may have been significant developments beyond that point. I will provide an overview of the state of quantum computing research and its potential, as well as some speculations about its future direction.

Current State of Quantum Computing Research and Development

Quantum Hardware Progress has been made in developing quantum processors, with companies like IBM, Google, Rigetti, and IonQ building and improving their quantum machines. Quantum bits or qubits, the basic unit of quantum information, are being implemented using various physical systems such as superconducting circuits, trapped ions, and topological qubits.

Quantum Algorithms Researchers are continuously exploring and developing quantum algorithms that outperform classical counterparts in specific tasks. Notably, Shor's algorithm for factoring large numbers and Grover's algorithm for unstructured search have demonstrated the potential for quantum speedup in certain problem domains.

Quantum Error Correction Quantum computers are highly susceptible to errors due to decoherence and noise in quantum systems. Efforts are underway to develop robust quantum error correction codes to improve the reliability of quantum computations.

Quantum Networking Quantum communication and networking protocols are being developed to enable secure communication and distributed quantum computing across different physical locations.

Hybrid Quantum-Classical Systems: Integrating quantum processing with classical computing is becoming more common to leverage the strengths of both paradigms.

Potential for Quantum Computing to Revolutionize Various Fields

Cryptography Quantum computers could potentially break classical cryptographic protocols based on factorization, posing a significant threat to current security systems. However, quantum-resistant cryptography methods are also being developed to counter this threat.

Optimization Quantum computing can potentially revolutionize optimization problems, leading to more efficient solutions in logistics, finance, and other fields.

Speculations about the Future Direction of Quantum Computing

Scaling Quantum Hardware:

 Researchers will continue to focus on increasing the number of qubits, reducing error rates, and improving coherence times to build more powerful and reliable quantum computers.

NISQ Era:

 The Noisy Intermediate-Scale Quantum (NISQ) era is expected to continue, wherein quantum devices are not yet fully error-corrected but can still solve valuable problems.

Quantum Software Development:

As quantum hardware evolves, there will be an increasing emphasis on developing quantum algorithms and software libraries to harness the potential of these devices effectively.

Quantum Cloud Services

 Companies may provide cloud-based quantum computing services, allowing broader access to quantum computing resources without requiring users to own and maintain quantum hardware.

Hybrid Approaches

Hybrid quantum-classical algorithms are likely to gain more attention, where quantum processors are used in conjunction with classical computers to solve complex problems efficiently.

Specialized Quantum Processors

We might see the emergence of specialized quantum processors optimized for specific applications or industries, similar to how GPUs are used for specific computational tasks.

Quantum Networks and Internet:

 Efforts to build quantum communication networks for secure data transmission and distributed quantum computing are likely to advance.

Quantum AI and Quantum Machine Learning:

The intersection of quantum computing and artificial intelligence could lead to breakthroughs in various AI tasks, such as natural language processing and optimization.

Conclusion

   - Recap of the key concepts and potential of quantum computing.

   - The importance of ongoing research and collaboration in the field.

   - Closing remarks on the promising future of quantum computing.

Note: This overview provides a substantial understanding of quantum computing, but it is important to note that the field is rapidly evolving, and new advancements and breakthroughs may have occurred beyond the knowledge cutoff date.